In order to understand as well as to predict the highly non linear mechanical response of natural and/or engineered discontinuous, blocky systems, comprising changing and evolving contact conditions and friction between their components or constituent parts, it is important to develop reliable analytical capabilities for simulations of such systems. In spite of extraordinary advances in nonlinear computational mechanics and simulations paradigms, the validation and verification of their predictive powers remains one of the main challenges in the field for their incorporation into industry relevant procedures. It can be safely argued that a major research attention in nonlinear structural dynamics today has noticeably moved from a reliable response of a specific structural system to a specific excitation towards a generic predictive capability for a class of structural configurations.

There are a number of structures that are inherently discontinuous, either as a matter of convenience (e.g. ease of construction in structural masonry or dry stone walling) or as a deliberate strategy to avoid extensive thermal stresses (e.g. graphite cores in Advanced Gas Cooled Reactors, AGR, in nuclear power plants). Often these structures are deliberately discontinuous, organised as stacked and/or interlocked assemblies with a regular pattern and technologically intended gaps and clearances, allowing for limited sliding and rocking in between contacts during their dynamic response. Frequently, these structural assemblies are by themselves a vital safety critical component of an entire structural system (or form a crucial part of) and there is a growing need to be capable of predicting their behavior under both static and dynamic (impact, seismic) conditions. This is particularly true with ageing and degradation of such systems (e.g. AGR cores), where the safety considerations with respect to their life extension may be paramount for the integrity assessment process of the entire plant operation.  Moreover, some of the safety critical ‘nonstructural’ components (e.g. large control cabinets) need to be treated as un-anchored blocky structures in their seismic assessment.

Structural reliability and integrity assessment procedures are largely formulated for continuum structures and their extension to consider discontinuous structural assemblies or configurations is not adequate. Therefore computational simulation frameworks for the analysis of blocky systems therefore often rely on some form of a homogenisation technique (simplified or complex), leading to a whole series of equivalent nonlinear continuum models. Such idealisations then allow for the structural integrity and reliability assessment procedures to follow well established routes, developed for continuum structures and supported by a series of well recognised benchmarks, both computational and experimental. In particular, the homogenisation process allows for a reasonably straightforward dynamic characterisation (e.g. spectral signature, eigen frequencies and mode shapes for response spectrum techniques in earthquake considerations are easily evaluated) of what are in reality discontinuous, ‘blocky’ structures, for which no eigen problem can be formulated.

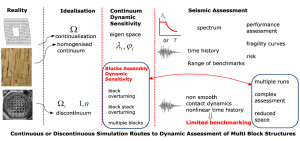In that context, it has been recognised that there are instances and situations where the homogenised, continuum description of multi block structures, comprising particulate and discontinuous cohesive and frictional solids is not an adequate model and the discrete nature of inherent or evolving discontinuities (with a regular or an irregular pattern) needs to be accounted for. In such analyses, ‘the whole’ is treated as an assembly of its ‘parts’, comprising multiple bodies (rigid or deformable), coming into and out of contact as the solution progresses. Bodies considered can be of an arbitrary shape and of an arbitrary level of deformability. The solution evolves in time and is typically treated as a very time consuming computationally intensive nonlinear contact dynamics problem, with a whole series of modelling assumptions regarding the treatment of the inter body contact and interface laws, which are often not well or not fully documented in the published literature. There are a number of different discontinuous modelling frameworks e.g. Discrete Element Method DEM, Combined DEM/FEM, MDEM Modified Distinct Element Method, Discontinuous Deformation Analysis DDA, Non Smooth Contact Dynamics NSCD. The differences are reflected in the manner these paradigms deal with the balance equations, the  definition of bodies geometry and contact detection, the imposition of contact constraints and/or the  contact law, with bodies deformability, potential fracturing and fragmentation, as well as the associated time stepping algorithms. Solutions to discontinuous problems are in general highly case dependent and there is a very limited range of controlled computational and experimental validation benchmarks of multi block assemblies in the literature. The solution may be highly sensitivity to the initial conditions, to the loss of symmetry and possible chaotic behaviour (e.g. bifurcation instances such as corner to corner contact or apparent buckling of a stack of particles/bodies which are very often an integral part of the nature of problems themselves. As a consequence, any associated integrity assessment procedures for multi block structures are on a much less firm ground that was the case with continuum structures, as they require numerous simulations and more complex probabilistic approaches. There is no formal way to a priori dynamically ‘characterise’ their sensitivities or ‘quasi resonance’ behavior of such multi block structures to assess in advance their potential susceptibility to dynamic excitations.

In the field of dynamic multibody contact and impact analysis the current state of the art for the industry relevant simulations (LS-DYNA, ABAQUS Explicit, UDEC/3DEC) stems back from the Discrete Element Method (DEM) originally proposed by Cundall and Strack and its variants, as a computationally simple, conditionally stable explicit time history approach based on repulsive springs, to prevent interpenetration of overlapping bodies. In a typical DEM implementation there is an analytical, one to one, relation between the interpenetration depth and the contact force (e.g. Hertz contact model) between the rigid or deformable bodies, enhanced with a damper element (viscoelasticity). For complex (e.g. non-convex, polyhedral) domains such (local) contact model becomes largely a numerical device, where careful tuning must be adopted in order to fit experimental evidence on bulk samples. Typically very stiff contact and/or interface laws follow, resulting in very inefficient time step stability limits and exceedingly lengthy run times for full scale simulations. Moreover, these stiff interface laws induce high frequency modes into the analysis, which are largely inconsequential for the overall behaviour. However, due to its computational simplicity, the DEM paradigm represents an industry standard to date.

Frequency response of multi body structures with regular patterns (similar to AGR graphite cores) comprises multiple impacts and shock waves within stiff, clearance separated blocky assembly. Impacts are essentially multi-scale phenomena. The physical resolution of impacts happens at a very fine time-space scale, while the observable engineering behavior happens at a much coarser time-space scale of gross rigid motion. In order to model multiple impacts within low resolution implicit approaches various algebraic impact laws have been proposed in literature. The time integration methodology which will be adopted in the context of this research is the Contact Dynamics (CD) method developed by Moreau and Jean, which effectively ignores the high frequency content of the contact interactions. Instead of a specified interpenetration-force relation, it employs a complementarity relation between the relative velocity and the contact force at an existing contact point: either the velocity is such that the bodies separate and the contact force is zero, or the force is such that interpenetration is prevented and in consequence the relative velocity is zero. This velocity-force complementarity relation is added as an algebraic constraint to the implicitly integrated momentum balance. Nonlinear contact problem is therefore solved implicitly at every time step in order to find the contact forces and the velocities of contacting blocks. Compared to the explicit time integration, where the small time and length scales in contact interactions are accounted for, in the non smooth contact dynamics the small scales and their effects are absorbed into contact laws, integrated at a larger scale. Although solving the contact problem is in itself time consuming, the overall simulation time may be significantly shorter than in the case of an equivalent explicit DEM simulation. Implicit velocity-impulse (or “non-smooth”) multi-body approaches are still a research niche within the field of multi-body dynamics, predominantly in Europe (largely research codes from specialised research groups – e.g. LMGC90 in Montpelier http://www.lmgc.univ-montp2.fr/LMGC90/LMGC90/Welcome_%21.html, Siconos at Lyon http://siconos.gforge.inria.fr/, MBSim at TU Munchen http://www.amm.mw.tum.de/1/home/, dynamY at ETH Zurich, http://www.zfm.ethz.ch/dynamY/index.html  etc). The preferred simulation paradigm within this proposal, SOLFEC, http://code.google.com/p/solfec/ is developed by Dr Koziara from Durham University, one of the partners in the current proposal. SOLFEC allows for modelling of a dynamic response of multibody systems with joints, contacts/impacts and friction, using a variety of kinematic models (e.g. rigid, pseudo-rigid, full or reduced order finite elements). Due to its computational efficiency, SOLFEC enables analyses of problems previously beyond the reach of implicit multibody approaches and thereby challenges the exclusive position of explicit paradigms in industry relevant applications.

Despite a number of very specialist benchmarks to deal with subtle issue on non smooth contact mechanics, there is a general lack of suitable, well controlled benchmarks problems to validate predictive capabilities of non smooth contact dynamics simulations relevant for multi block structural configurations, with a regular construction pattern and/or clearances. Closed form analytical benchmarks are largely restricted to two dimensional single or double rigid block structural assemblies, typically concerned with rocking and overturning conditions due to harmonic or step base excitation of specific amplitudes. Furthermore, for simplicity, the contact friction is assumed high, in order to prevent complexities associated with combined rocking and sliding. Limited dynamic characterisation of a single rigid block structure based on geometry similarity arguments alone has been achieved as a useful structural performance sensitivity attribute for any block geometry. An extension of such ideas to generic predictive capability for a class of multi block structural configurations has not been done. Experimental benchmarks are also often a byproduct of a study of a specific problem and structural configuration and a specified excitation. This proposal is geared towards a generic predictive simulation capability for a class of structural configurations, rather than for specific cases only. Validations of computational simulations are also largely problem specific, as they again involves suitable tuning of modeling parameters (restitution coefficient, friction, damping) to fit observable findings from the experiment, whilst the generalisation of the modeling parameters remains largely elusive.